Problem Statement
We have to implement a productExceptSelf function that takes an integer array nums as input and returns another array answer as output. The element answer[i] will be the product of all elements in inputArray except inputArray[i].

The implementation should not contain a division (/) operation because the answer array could also be created by iterating over all elements in inputArray and dividing them from the product of the complete array.
Brute Force Solution
The brute-force solution to this problem could be implemented using nested loops. Where the first loop will select an element from the array and the second loop will be used to calculate the product without the element from the first loop.
Psuedo-code for the Brute Force Solution
answer = []
loop index on nums
product = 1
loop index2 on nums
if index!=index2
product *= nums[index2]
answer.append(product)
return answer
Time Complexity Analysis
Best Case Scenario
The brute-force solution will return the answer array in $O(n^2)$ time for the best-case input. Since both the loops will iterate completely over the nums array.
Worst Case Scenario
The worst-case scenario will also take $O(n^2)$ to return the solution.
Space Complexity Analysis
The answer array will require additional $O(n)$ memory.
Code for the Brute Force Solution
package main
import "fmt"
func productExceptSelf(nums []int)([]int){
answer := []int{}
for index:=0;index<len(nums);index++{
product := 1
for index2:=0;index2<len(nums);index2++{
// Skip the element selected by the outer loop
if index!=index2{
product *= nums[index2]
}
}
answer = append(answer, product)
}
return answer
}
func main(){
nums := []int{1, 2, 3, 4}
fmt.Println("Product Except Self:", productExceptSelf(nums))
nums = []int{45, 34, 67, 86, 23}
fmt.Println("Product Except Self:", productExceptSelf(nums))
}
// Output
// Product Except Self: [24 12 8 6]
// Product Except Self: [4505884 5963670 3026340 2357730 8815860]
Optimized Solution
If we have to improve the time complexity of brute-force solution then we have to think of something other than nested loops.
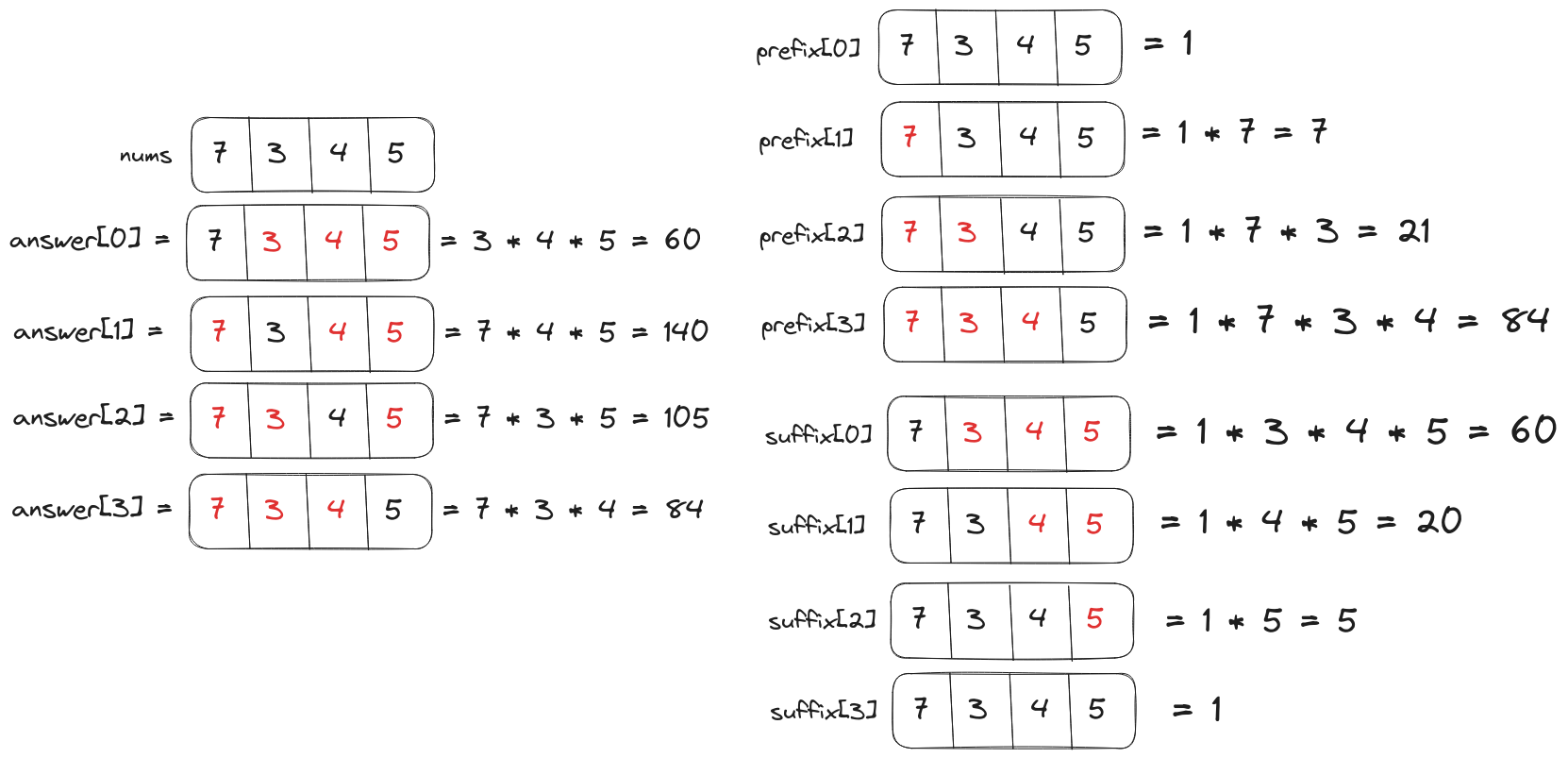
The “product except self” for an element nums[i] refers to the product of all elements before and after nums[i] i.e. answer[i] = nums[0:i-1] * nums[i+1:]. Thus, we can implement the productExceptSelf function with $O(n)$ time complexity if we calculate two arrays prefix and suffix where
prefix[i]is the product of all elements beforenums[i]

suffix[i]is the product of all elements afternums[i]

and multiply them to create the answer array.
Psuedo code for the Optimized Solution
prefix = []
loop index on nums
prefixProduct = 1
prefix.append(prefixProduct)
prefixProduct *= nums[index]
suffix = []
loop index from length(nums)-1 to 0
suffixProduct = 1
suffix.append_at_start(suffixProduct)
suffixProduct *= nums[index]
answer = []
loop index on prefix
answer.append(prefix[index]*suffix[index])
return answer
Time Complexity Analysis
Best Case Scenario
The optimized solution will return the answer array in $O(n)$ time (generalized from $O(3n)$) since the time complexity of iterating over all three arrays (prefix, suffix, and answer) is $O(n)$.
Worst Case Scenario
The time complexity of iterating over arrays in worst-case input is the same as in the best-case scenario. Thus, the total time complexity of the function remains the same i.e. $O(n)$.
Space Complexity Analysis
To store the prefix, suffix, and answer array we will need additional $O(3n)$ memory.
We can improve the space complexity if we use a single array for storing the products of prefix and suffix and return it as the answer.
Code for the Optimized Solution
package main
import "fmt"
func productExceptSelf(nums []int)([]int){
prefix := []int{}
prefixProduct := 1
for index:=0;index<len(nums);index++{
prefix = append(prefix, prefixProduct)
prefixProduct *= nums[index]
}
suffix := []int{}
suffixProduct := 1
// Loop over the nums array in reverse
// starting from the last element
for index:=(len(nums)-1);index>(-1);index--{
// Append the element at the start
// rather than at the end
suffix = append([]int{suffixProduct}, suffix...)
suffixProduct *= nums[index]
}
answer := []int{}
for index:=0;index<len(prefix);index++{
// Multiply prefix and suffix elements
// to create the answer array
answer = append(answer, prefix[index]*suffix[index])
}
return answer
}
func main(){
nums := []int{4, 2, 3, 7}
fmt.Println("Product Except Self:", productExceptSelf(nums))
nums = []int{45, 34, 67, 86, 23}
fmt.Println("Product Except Self:", productExceptSelf(nums))
}
// Output
// Product Except Self: [42 84 56 24]
// Product Except Self: [4505884 5963670 3026340 2357730 8815860]
Code for the Optimized Solution (Constant Space Complexity)
Assuming the memory space required by the answer array is constant i.e. $O(1)$.
package main
import "fmt"
func productExceptSelf(nums []int)([]int){
answer := []int{}
// Fill up the answer array with prefixes
prefixProduct := 1
for index:=0;index<len(nums);index++{
answer = append(answer, prefixProduct)
prefixProduct *= nums[index]
}
// Multiply suffixes with the existing
// values in the answer array i.e. prefixes
suffixProduct := 1
for index:=(len(nums)-1);index>(-1);index--{
answer[index] *= suffixProduct
suffixProduct *= nums[index]
}
return answer
}
func main(){
nums := []int{4, 2, 3, 7}
fmt.Println("Product Except Self:", productExceptSelf(nums))
nums = []int{45, 34, 67, 86, 23}
fmt.Println("Product Except Self:", productExceptSelf(nums))
}
// Output
// Product Except Self: [42 84 56 24]
// Product Except Self: [4505884 5963670 3026340 2357730 8815860]
Thank you for taking the time to read this blog post! If you found this content valuable and would like to stay updated with my latest posts consider subscribing to my RSS Feed.
Resources
238. Product of Array Except Self
Product of Array Except Self - Leetcode 238 - Python